Preamble Link to heading
Ever since learning about Existential Graphs (EGs) from a talk given by Bram Van Heuveln [1] at the New York Capital Region Logic Reading Group; I’ve had Existential Graphs on my mind a lot. Not only due to their very real ability as a tool for helping students learn logic and the benefits they offer as a formal system in overcoming an inference rule count vs proof length tradeoff, but also due to how magical they feel. Complex Existential Graphs in the Beta and Gama systems such as those found in [2] can start looking like magic circles strait out of a grimoire…
Unfortunately there do not seem to be many concise resources for learning existential graphs on the internet. In this post I will outline my understanding of representation simplest Existential Graph system, Alpha, assuming the reader has only a basic familiarity with propositional logic.
Representing Propositional Formulae as Existential Graphs Link to heading
Existential Graphs can be though of as a diagrammatic/visual means of representing logical statements and reasoning over them. The Alpha system can be thought of as a limited two dimensional representation for propositional logic, where the items of investigation are propositional statements (sentences that may be true or false) and the relations between them. The first step to getting a handle on existential graphs in the alpha system is to understand how to build and interpret them.
To do this we will go through how each of the propositional connectives may be represented as an existential graph one by one. There are five types of propositional compound operators that people typically care about (at least enough that they make it into the most popular inference systems, sorry XOR):
| Name | Symbolically | Meaning | Important Logical Equivalence |
|---|---|---|---|
| Atomic Statement | $A$ | A is true | |
| Logical Not (NOT) | $\lnot A$ | A is not true | |
| Logical And (AND) | $A \land B$ | Both A and B are true | |
| Logical Or (OR) | $A \lor B$ | Either A or B is true | $\lnot (\lnot A \land \lnot B)$ |
| Conditional (IF) | $A \rightarrow B$ | If A is true then B is true | $\lnot A \lor B$ |
| Biconditional (IFF) | $A \leftrightarrow B$ | A is true if and only if B is True | $(A \rightarrow B) \land (B \rightarrow A)$ |
Atomic Propositions and the Sheet of Assertion Link to heading
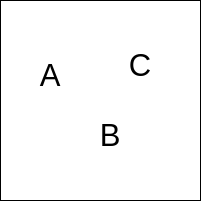
To represent an atomic statement $A$ in propositional logic, one merely represents it as a “1d” propositional formula “$A$”. Existential graphs however are represented in 2d space on what is known as the “Sheet of Assertion”, which we draw as a square. To represent an atomic proposition $A$ as an existential graph, we may place it anywhere on the sheet of assertion.

Note that the location of the statement on the sheet of assertion is irrelevant, All of the following existential graphs are regarded as identical.

Logical And Link to heading
If we want to assert a conjunction of multiple statements $A$, $B$, $C$ in propositional logic we may use the AND operator ($\land$) between them like so, “$A \land B \land C$”. Semantically, we read this as “A and B and C are all true”. To represent this in an existential graph, we can individually assert each statement on the sheet of assertion.
We can generalize this notion to any number of statements. The following represent “$A \land B$”, “$A \land B \land C \land D$” respectively.
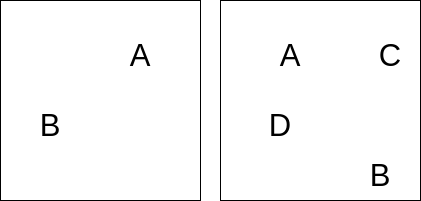
Note that the order and location of the conjuncts is irrelevant, these could just as easily be read “$B \land A$” for the left and any permutation of $A, B, C, D$ for the right.
Logical Not and Cuts Link to heading
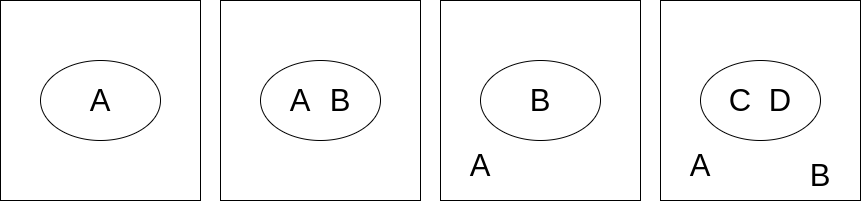
To represent the negation of some statement $A$ in propositional logic, we can prefix it with a $\lnot$. We can interpret this as introducing some form of inner context for 1d formulae in which everything inside a $\lnot(\cdots)$ is asserted to be false. Since existential graphs are 2d, we need some way of representing what a negated context two dimensionally. This is done using a “Cut” which is represented by drawing a connected boundary on the sheet of assertion, often written represented by a circle or oval. Everything inside the cut is taken to be negated.
From left to right:
- $\lnot A$,
- $\lnot (A \land B)$
- $A \land \lnot B$
- $A \land B \land \lnot (C \land D)$
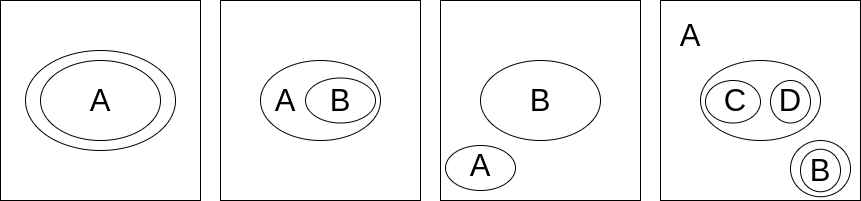
Note that just as we can have negated formulae inside of negated formulae in propositional logic (things like $\lnot (A \land \lnot B)$), we can have cuts inside of cuts inside in existential graphs.
From left to right:
- $ \lnot \lnot A $
- $ \lnot (A \land \lnot B) $
- $\lnot A \land \lnot B$,
- $A \land \lnot \lnot B \land \lnot (\lnot C \land \lnot D)$
Logical Or Link to heading
So far we have introduced ways to represent conjunction via multiple assertion and negation as cuts in existential graphs. These are actually the only two representational features provided by the alpha system. So how can we represent other compound operators such as OR in existential graphs? This is where the property of functional completeness of AND and NOT comes into play. In short, AND and NOT are the only operators you need to represent all possible truth tables [3]. That is, any other logical operator can be defined solely in terms of ANDs and NOTs. To represent $A \lor B$ in terms of AND and NOT we can use the equivalent formula $\lnot (\lnot A \land \lnot B)$. The equivalence of this formulae to OR can be proven easily using De Morgan’s laws or using a truth table.
With this equivalence in place, we can now use the tools of existential graphs we have seen so far to represent OR.
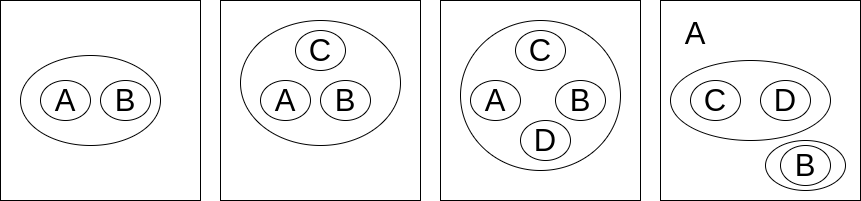
From left to right:
- $A \lor B$
- $A \lor B \lor C$
- $A \lor B \lor C \lor D$
- $A \land \lnot \lnot B \land (C \lor D)$
Note:
- The rightmost EG is the same as the rightmost EG from the NOT section. By understanding how OR may be represented, we attain a more human understandable meaning of the graph beyond the conjuncts and negations.
- The pattern in the left three EGs holds for an arbitrary number of conjuncts, this can easily be proven using De Morgan’s laws. $$ \lnot (\lnot a_1 \land \lnot a_2 \land … \land \lnot a_n) \equiv a_1 \lor a_2 \lor … \lor a_n $$
Conditionals Link to heading
Just like OR, IF can be represented solely in terms of ANDs and NOTs. Perhaps the most famous equivalence of IF is the Or-and-if relation which states that $A \rightarrow B$ is logically equivalent to $\lnot A \lor B$. This gives us IF in terms of NOT and OR, to put it in terms of NOT and AND we can apply the definition of OR from the previous section to obtain $\lnot(\lnot\lnot A \land \lnot B)$. Finally we can cancel the double negation to obtain just $\lnot(A \land \lnot B)$. Using this we can represent IF in an existential graph.
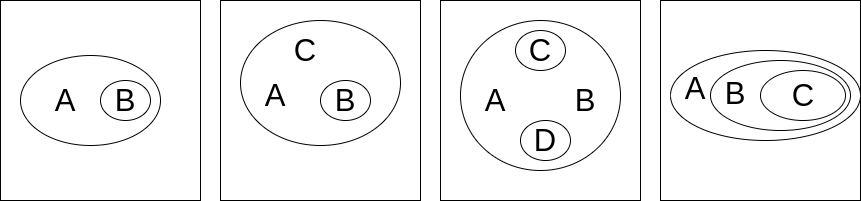 Each of these can have multiple logically equivalent PL translations of which I list a few here.
From left to right:
Each of these can have multiple logically equivalent PL translations of which I list a few here.
From left to right:
- $\lnot(A \land \lnot B)$
- $A \rightarrow B$
- $\lnot (A \land C \land \lnot B)$
- $(A \land C) \rightarrow B$
- $A \rightarrow (C \rightarrow B)$
- $C \rightarrow (A \rightarrow B)$
- $\lnot (A \land B \land \lnot C \land \lnot D)$
- $(A \land B) \rightarrow (C \lor D)$
- $A \rightarrow (B \rightarrow (C \lor D))$
- $B \rightarrow (A \rightarrow (C \lor D))$
- $\lnot (A \land \lnot (B \land \lnot C))$
- $A \rightarrow (B \land \lnot C)$
- $A \rightarrow \lnot (B \rightarrow C)$
Biconditionals Link to heading
IFF, if and only if, is defined as $(A \rightarrow B) \land (B \rightarrow A)$. Using our existential graph for IF, we can write IFF. A common alternative representation for IFF, $(A \land B) \lor (\lnot A \land \lnot B)$ can also be used;Via our definition of OR we can rewrite this as in terms of AND and NOT as $\lnot (\lnot (A \land B) \land \lnot(\lnot A \land \lnot B))$. We will later see this definition is equivalent to the first and prove it using the rules of inference of Alpha.
Two equivalent formalisms of IFF:
Left: $(A \rightarrow B) \land (B \rightarrow A) \equiv \lnot (A \land \lnot B) \land \lnot (B \land \lnot A)$
Right: $(A \land B) \lor (\lnot A \land \lnot B) \equiv \lnot (\lnot (A \land B) \land \lnot(\lnot A \land \lnot B))$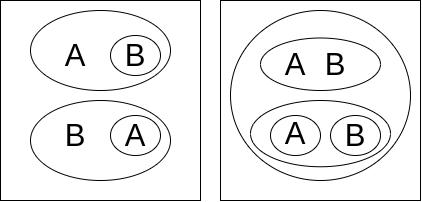
Conclusion Link to heading
In this post we’ve looked at how propositional logic statements may be translated to Alpha EGs and how Alpha EGs may be translated back into propositional logic. While this 2d representation of propositional logic statements is very interesting visually, what benefits does it provide? In the next post in this series we will explore the inference rules by which we may reason in the Alpha system.
References Link to heading
[1] Van Heuveln, B. (2023, March 29). Existential Graphs [public talk]. New York Capital Region Logic Reading Group, NY, USA. Retrieved July 28, 2023, from
https://homepages.hass.rpi.edu/heuveb/Teaching/Logic/CompLogic/Web/Presentations/EG.pdf.
[2] Roberts, D. D. (1973). The Existential Graphs of Charles S. Peirce. (T. A. Sebeok, Ed.) (Vol. 27, Ser. Approaches to Semiotics). Mouton.
[3] Rozek, B. (2023, May 30). Functional Completeness [web blog]. Retrieved July 28, 2023, from
https://brandonrozek.com/blog/functional-completeness/.