Subgraphs, Levels, and Nested Levels Link to heading
Last post we looked at what Alpha Existential Graphs represent and how we may build them. In the next post we will look at how we may reason with them using rules of inference. However, before we discuss inference rules for existential graphs, we need to discuss three important “syntactic” (2d syntactic!) concepts in existential graphs which are referenced in the definition of most of our rules of inference. These concepts are Subgraphs, Levels, and Nested Levels.
Subgraphs Link to heading
The notion of subgraphs is best understood via an example, the following EG representing $A \rightarrow B$ has five obvious subgraphs, including the graph itself. (Note: We may also consider the empty EG representing the logical constant True to be a subgraph of every level, but do not depict this.)
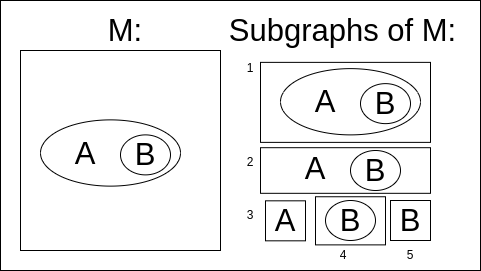
How can we formalize this better? One way is to map an existential graph to an n-ary tree structure. The sheet of assertion is the root, atoms are leafs, and cuts may either be leaves or have children. In this representation a subgraph corresponds a subset of children on a given level of the tree. (Note: The empty set $\empty$ is a subset of children on any level, corresponding to the idea that the the empty EG representing the logical constant True is a subgraph on any level)
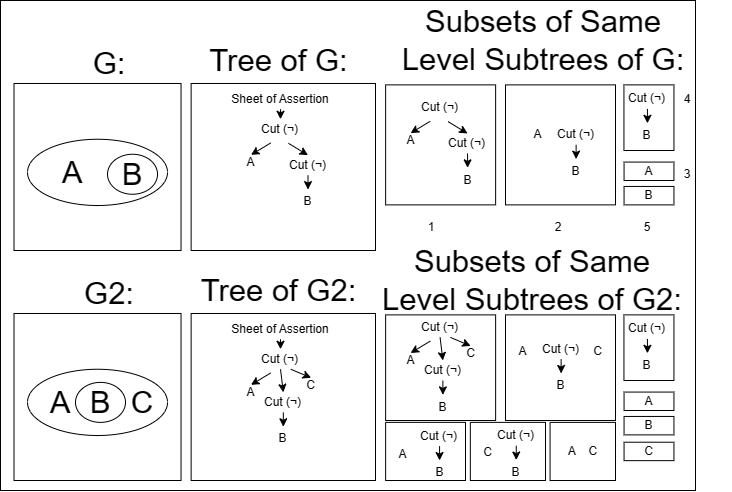
In $G$ we observe that each subset on each level corresponds directly with one of the subgraphs from the previous figure. When written symbolically, $G$ has the following subgraphs $\{\lnot(A \land \lnot B)\}$, $\{A, \lnot B\}$, $\{A\}$, $\{\lnot B\}$, $\{B\}$, $\empty$ (Note $\empty$ not pictured).
In $G2$ we need to account for every subset of the children on the first cut as a subgraph. Symbolically we would say the subgraphs of $G2$ are $\{\lnot(A \land \lnot B \land C)\}$, $\{A, \lnot B, C\}$ are $\{A, \lnot B, C\}$, $\{A, \lnot B\}$, $\{A, C\}$, $\{\lnot B, C\}$, $\{A\}$, $\{\lnot B\}$, $\{C\}$, $\{B\}$, $\empty$.
For a deeper look at this can be formalized see here.
Levels Link to heading
Level is a property of subgraphs, the level of a subgraph is the number of cuts you need to pass through from the sheet of assertion to reach that subgraph. We can formalize this using the tree representation used to formalize subgraphs; The level of a subgraph is the level of the tree it is formed at, with the sheet of assertion as level 0. More intuitively, we can visualize the concept of level as a Topographic map with cuts as contour lines marking what level a subgraph is at.
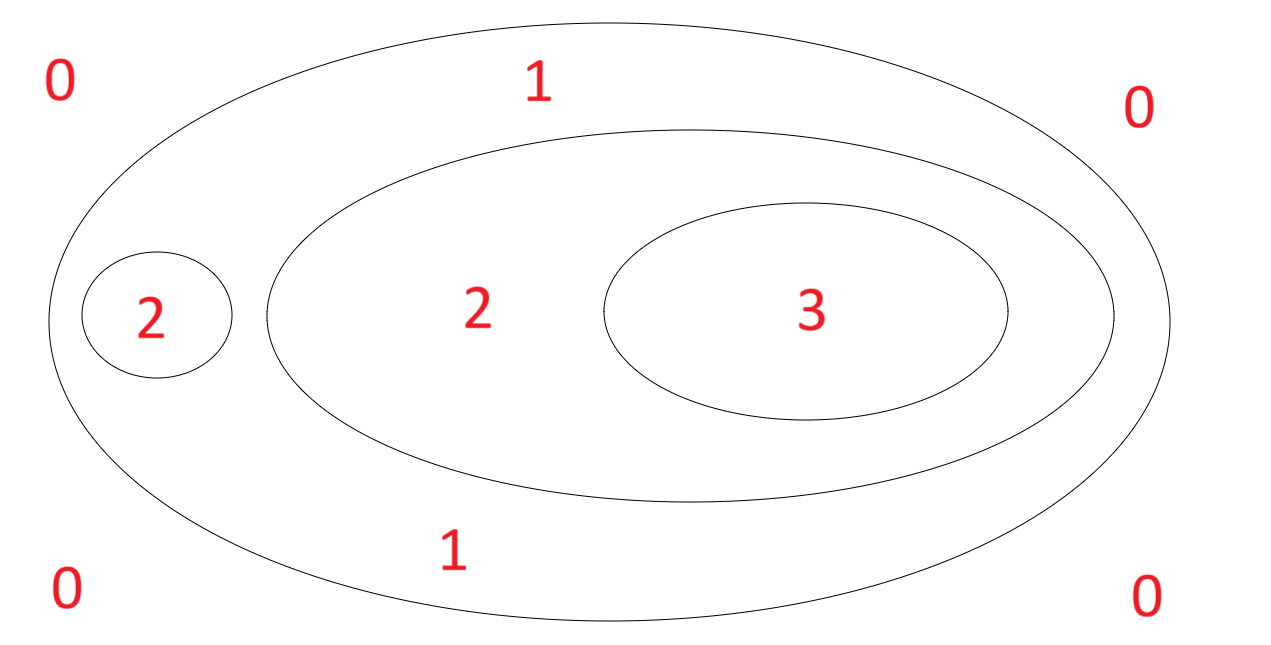
For example the subgraph consisting of the level 3 cut is said to be on level 2, and the top level cut is said to be on level 0.
In the above example for $G2$:
- The level of $\{\lnot(A \land \lnot B \land C)\}$ is 0,
- $\{A, \lnot B, C\}$, $\{A, \lnot B, C\}$, $\{A, \lnot B\}$, $\{A, C\}$, $\{\lnot B, C\}$, $\{A\}$, $\{\lnot B\}$, $\{C\}$, are all at level 1.
- $\{B\}$ is at level 2.
- $\empty$ is present on all levels.
Nested Levels Link to heading
Formally, A subgraph $P$ is at a nested level with respect to another subgraph $Q$ iff one can get from $Q$ to $P$ by going inside (lower level to higher level) zero or more cuts, but without going outside (higher level to lower level) any cuts. In other words, thinking back to our topography example, a subgraph $P$ is at nested level with respect to $Q$ if you can reach it by never going downhill (moving to a level smaller than $Q$s).
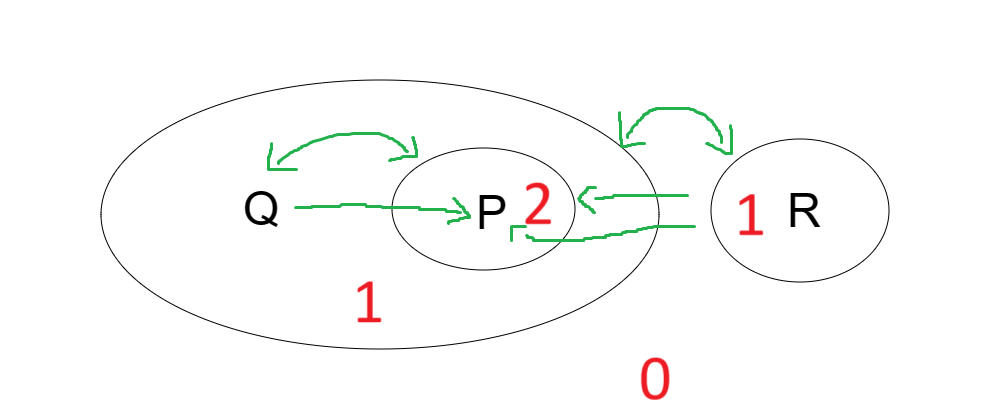 In this figure green arrows represent some possible nested level relations (not all are pictured, can you find the remaining non-$\empty$ two?). $P$ is at a nested level with respect to $Q$ because to reach it we are going from a lower level to a higher level. Note now that $Q$ and $(P)$ are both considered to be at a nested level relation to each other, this property holds in general, any two subgraphs on the same level are considered to be nested in relation to each other, just as $(Q (P))$ and $(R)$ are. All subgraphs of $(Q (P))$ are nested in relation to $(R)$. Note that it appears nothing is at a nested level with respect to $P$ or $R$ as they are the sole atoms inside their cuts. However, we must remember that $\empty$ is a subgraph of everything, hence $P$ and $R$ (and all other subgraphs) are nested with respect to $\empty$ and vice versa.
In this figure green arrows represent some possible nested level relations (not all are pictured, can you find the remaining non-$\empty$ two?). $P$ is at a nested level with respect to $Q$ because to reach it we are going from a lower level to a higher level. Note now that $Q$ and $(P)$ are both considered to be at a nested level relation to each other, this property holds in general, any two subgraphs on the same level are considered to be nested in relation to each other, just as $(Q (P))$ and $(R)$ are. All subgraphs of $(Q (P))$ are nested in relation to $(R)$. Note that it appears nothing is at a nested level with respect to $P$ or $R$ as they are the sole atoms inside their cuts. However, we must remember that $\empty$ is a subgraph of everything, hence $P$ and $R$ (and all other subgraphs) are nested with respect to $\empty$ and vice versa.