In this post we continue looking at the inference rules of alpha existential graphs, in particular we look at the final two rules of inference, Iteration and Deiteration, and provide some examples.
Iteration and Deiteration Link to heading
This inference rule states we can introduce a copy of a subgraph $\phi$ at any nested level in relation to $\phi$. Recall that we say a subgraph $\psi$ is at a nested level with respect to $\phi$ iff $\psi$ and $\phi$ are on the same level or $\psi$ can be reached from $\phi$ by only going inside of cuts, for a refresher see the post where I define nested levels in more detail. If we take the tree based view of AEGs, the Iteration rule says we can insert a subtree (or set of subtrees) as its own sibling, or as a descendant of any of its siblings. Deiteration is just the inverse of iteration. It allows us to remove a subgraph as long as a copy of that subgraph can be reached by only going outside of cuts.
For the most basic example, here we iterate $A$ onto an odd level and even level.
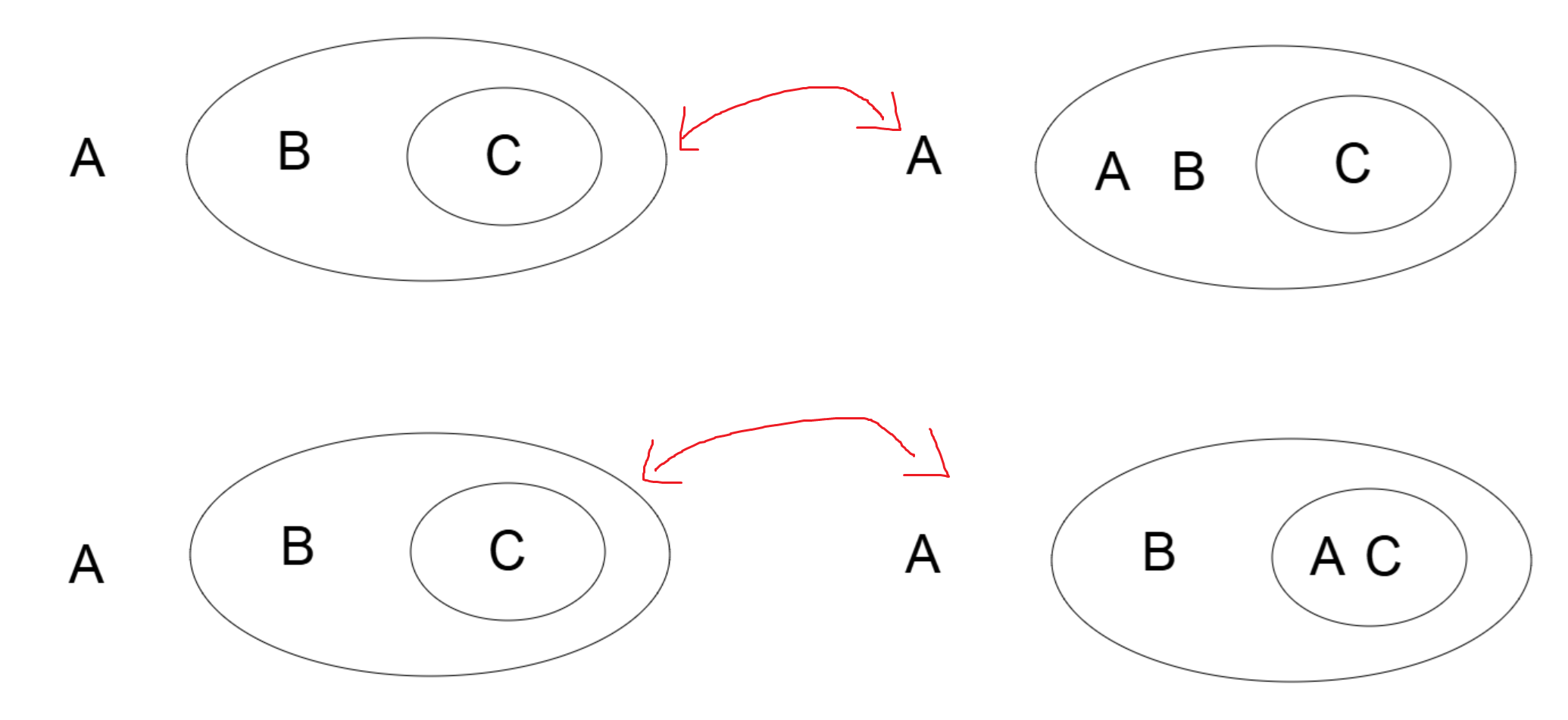
What does iteration correspond to in propositional calculus? Formally it corresponds to the forward direction of absorption which we state as a propositional theorem: $$ (A \rightarrow B) \Leftrightarrow (A \rightarrow (A \land B)) $$ This gives us a very narrow reading of absorption, to show how this can generalize to the iteration rule, we will instead look at the following two variants of the absorption rule. These variants can be verified via truth table. The first variant allows us to distribute or pull out a conjunct from the antecedent of a conditional. $$ (A \land (B \rightarrow C)) \Leftrightarrow (A \land ((A \land B) \rightarrow C)) $$ The second variant allows us to distribute or pull out a conjunct from the consequent of a conditional. $$ (A \land (B \rightarrow C)) \Leftrightarrow (A \land (B \rightarrow (A \land C))) $$ The first variant corresponds to iterating/deiterating onto odd levels while the second corresponds to iterating/deiterating onto even levels. These absorption rules actually correspond to the iteration and deiteration we see in the first figure!
It should be clear that if we replace $B$ or $C$ with another conditional, corresponding to another nested level in an AEG, we can perform any number of applications of these absorption rule rewrites to insert the outermost $A$ into any nested level, or can perform this procedure in reverse to remove $A$ from any nested level for deiteration. We could also replace $A$ with any arbitrarily complex graph.
Here is an example of iterating and or deiterating a large graph into a further nested level (3rd level).
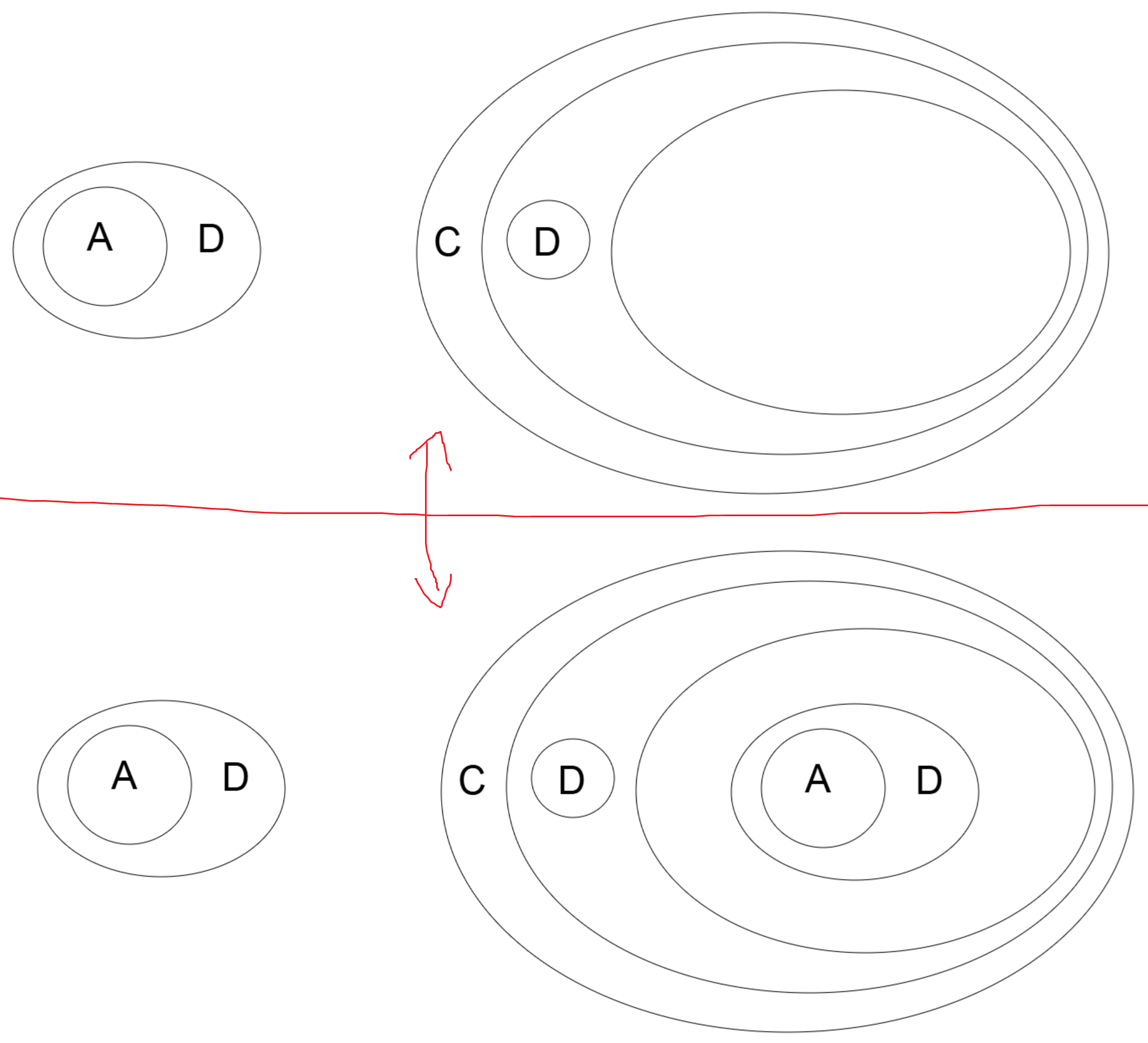
This wraps up the brief post on iteration and deiteration. In the future it would be nice to take a look at proving some common theorems with the rules we have learned so far.
Since the start of this series, A team of programmers at the University at Albany under my stewardship has finished a wonderful application for constructing and doing proofs with Alpha Existential Graphs. I strongly recommend checking it out!
References Link to heading
[1] Van Heuveln, B. (2002, June 6). Formalizing Alpha: Soundness and Completeness [web slides]. Retrieved July 31, 2023, from
https://homepages.hass.rpi.edu/heuveb/Research/EG/details.html.